Basic RGB clustering

Rev. 2/27/2023 LRM

Although I'm still totally happy with my basic approach of clustering multichannel images by reducing them to a simple RGB image -- using no process other than simply looking at three channels at a time -- it occurred to me that I could also reduce the dimensionality of the data by just using PCA like a normal person would. So that's what I've done here using a modified, PCA-based version of my basic RGB clustering script.

While last time I did the clustering on a RGB image composed of three channels for Fe, Mg, and Si K-alpha X-rays, this time I am using all 10 of the auto-detected elements from the hyperspectral EDS map (as shown in the above animation). Note that Na, Al, and K -- not accounted for previously -- show up in high concentrations in the fine-grained Si-rich regions between the larger more Ca- and Mg-rich grains (pyroxene and olivine respectively). Maybe a mixture of plagioclase, orthoclase, and quartz?

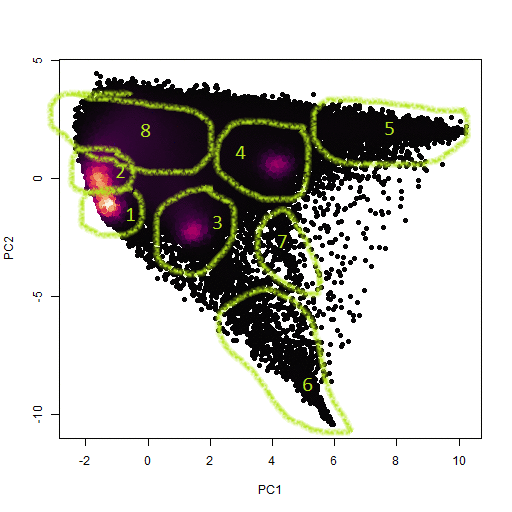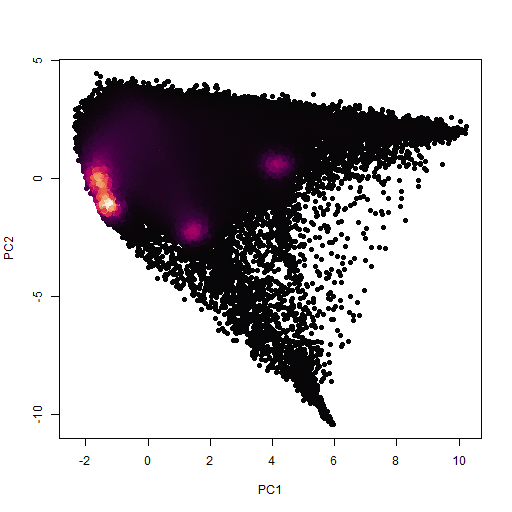
This time, instead of going through the whole rigmarole of stacked scatter and ternary plots, I just used R's prcomp function to calculate the principal components of the dataset. A plot of PC's 1 and 2 clearly divides the data into nice clumps. What's even more encouraging is that there are more clusters immediately visible in the plot than there were in the RGB scatter plots.

As before, I just used my own locate_poly function to manually identify the clusters using a downsampled version of the PCA scatter plot, and then transferred the located points onto a template raster object (below).

One more thing I noticed is that some of the clusters don't show up as high density areas (purple), but they do show up as pointy structures in the scatterplot which seem to be some kind of endmember concentration with many pixels mixed between it and the other clusters. I think these must represent phases with grain sized approaching the pixel size. This theory does seem to be somewhat confirmed in that cluster 5 shows up as small grains upon further inspection (also below). Clusters 6 and 7 are bigger and also seem to be mixed with adjacent grains in the sense that they seem to represent pore space.

So then what are the clusters anyway? Here's my attempt to identify them:

Comparing the PCA method to the RGB method, I could conclude that the PCA method is easier and better. The main difference I notice is that the RGB method subdivided the Mg-rich olivine into two phases while not separating the two OPX core and rim phases. I think this makes sense because the elements chosen more or less arbitrarily to occupy the color channels will be disproportionately weighted more heavily than the other elements. I also like that the PCA method allowed me to isolate the BS phases related to sample preparation artefacts more easily so that they could be specifically ignored. I guess I've learned my lesson -- PCA is what you need to cluster multichannel images!

Finally, to bring this exploration "full circle," I took the three most significant components PC1, PC2, and PC3 and converted them into an RGB image shown below.

Rev. 2/22/2023 LRM

Lately I've been trying to wrap my mind around the problem of using multi-channel images of rock samples to segment the analyzed area according to the minerals in the sample. With one channel, it's a simple thresholding problem. With two channels, clusters can be identified with a scatter plot. Clusters in three channels can be identified similarly using a ternary plot. But what about four or more channels?

Here's where one might think about clustering using k-means, HCA, or some other statistical model (ANNs?) for classification. But more sophisticated models require more sophisticated optimization, so the choice of a fancy clustering model requires demonstrating that it can out-perform a simpler model.

So here's my proposed solution: reduce the dataset to three channels, make an RGB image, and do clustering on the image. Do I think this is the best solution? No. Well, yes. Or maybe? Consider this like the "null hypothesis" in the sense that we can only accept a more complex solution after it can be demonstrated to out-perform my "null solution." So, yes for now.

Here's an example image from EDS data collected on a basalt from near Mammoth Lakes, CA. The red, green, and blue channels correspond to Fe, Mg, and Si respectively. The image was made in ImageJ by... eh, nevermind.

Ok, so let's use the the best, most readily-available neural network to segment the image: the human brain! I think I see a green plase, a dark blue phase, a light blue phase, and a red phase. There -- what do I win?

Ok, so where them clusters at? Here's a couple of 2d-scatter plots colored as in the image. looks like there is a lot of noise, but the data seem to cluster around a few endmember locations, similar to the clusters immediately visible in the image.

Yes, this is way better: using a ternary plot, the clusters can now be clearly separated on a single image. Now all I have to do is use my locate_poly function to manually identify the points...

...and here are the clusters! Note that closters 0, 1, 2, 3, 4, and 5 are unsegmented points, the green phase, a lighter green phase that I identified subsequently, the red phase, the light blue phase, and the dark blue phase respectively. The number of unclassified points can pretty much be ignored since it doesn't account for very many pixels.